Jakob Paul Zimmermann

Research

At FU Berlin with Georg Loho, I investigate the geometry of the Newton Polytopes of Neural Networks and develop new Explainable AI (XAI) methods using the Difference-of-Convex decomposition of Neural Networks. I also study how to learn the support function of polytopes with Neural Networks.

At Fraunhofer IOSB, I work on runtime monitoring of image recognition models and representation learning. I develop a new monitoring approach that is knowledge-guided and works on internal representations of image recognition models and embedding models such as DINO.

Goals

I want machine learning models to be:

• Safe and Reliable – especially in critical applications and under distribution shifts
• Interpretable – transparent decision-making that humans can understand and verify
• Aligned – reasoning that mirrors human intuition and values

I investigate how geometric and mathematical structures in Neural Networks can help achieve these properties, and how to explain the decision-making of Neural Networks in a way understandable to humans.

Publications

Preprints

Hidden Monotonicity: Explaining Deep Neural Networks via their DC Decomposition

(under submission)

arXiv:2601.07700, January 2026

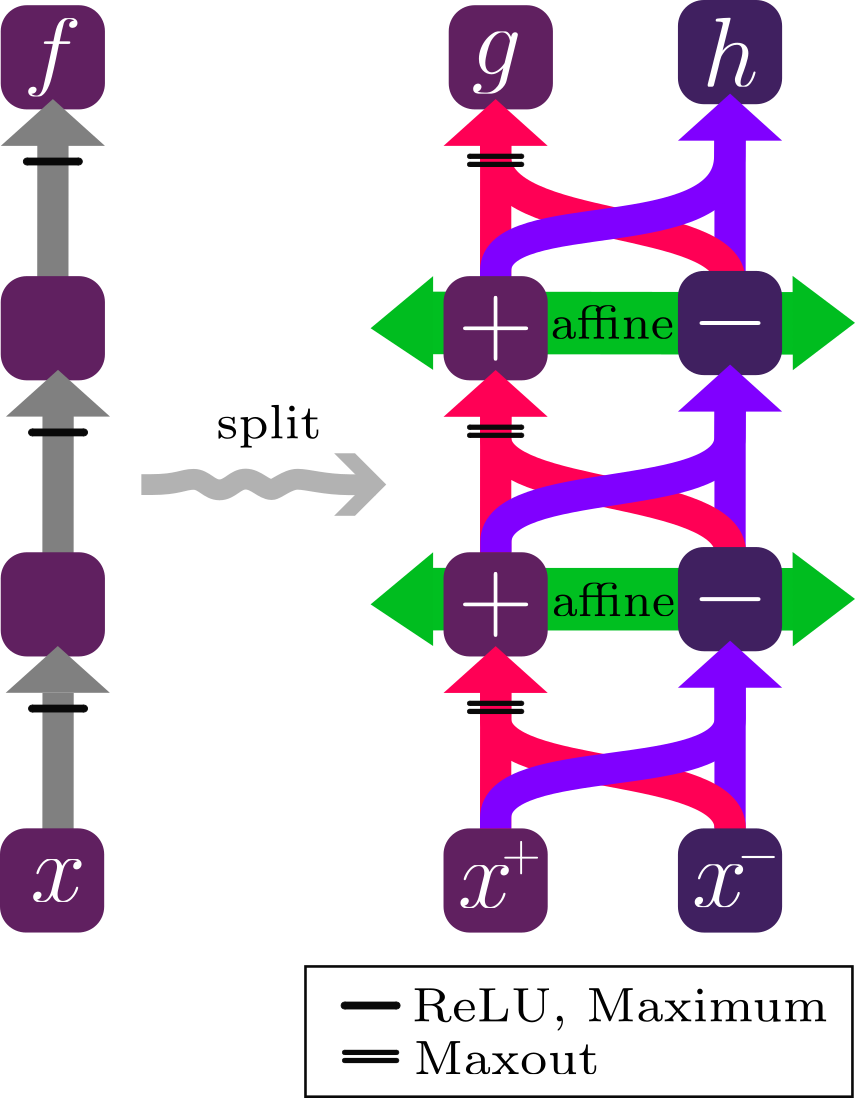
We propose an algorithm to decompose any ReLU Neural Network (CNN, MLP, ResNet) into a difference of two monotone and convex Maxout networks and to stabilize the forward and backward pass through this decomposition. This provides a principled approach for Explainable AI, enabling separate analysis of positive and negative contributions to the network output. Our proposed saliency methods - SplitCAM and SplitLRP - improve on SOTA results on both VGG16 and Resnet18 networks on ImageNet-S across all Quantus saliency metric categories.

Mathematical Interests

Stochastics, Statistical Learning, Discrete Geometry, Extremal combinatorics, Turán-type problems.

In a recent master project I investigated the bipartite Turán problem on cographs (graphs with no induced P₄) and fully classified the edge-maximal cographs with respect to not containing certain bicliques. These extremal cographs turn out to be star-shaped, highly symmetrical and beautiful.

Education